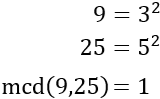Índice:
- Calculadora de mcm y mcd
- Problemas resueltos de mcd
Calculadora de mcm y mcd
Introducir 2 o 3 números para calcular su mcm y su mcd.
| Números: | |||
| mcm = | |||
| mcd = | |||
Problemas resueltos de mcd
A continuación, resolvemos 8 problemas de aplicación del mcd. Otros problemas relacionados:
- Mínimo común múltiplo
- Problemas mixtos de mcm y mcd
- Problemas teóricos de mcm y mcd
- Mínimo común múltiplo (2)
- Máximo común divisor (2)
- Problemas mixtos de mcm y mcd (2)
- Problemas mixtos de mcm y mcd (3)
Problema 1
Calcular el máximo común divisor (mcd) de los números 60, 72 y 90.
Solución
El mcd se calcula del mismo modo tanto para dos como para más números.
Escribimos los números como productos de potencias de primos:
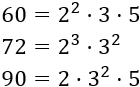
El mcd se calcula multiplicando las bases comunes al menor exponente. Las bases comunes son 2 y 3. Los exponentes menores son 1 para la base 2 y 1 para la base 3.
Por tanto, el mcd es 6 ya que
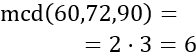
Problema 2
Carlos tiene una caja con 200 caramelos de fresa y 175 de limón. Quiere hacer bolsitas iguales que contengan caramelos de fresa y de limón para repartirlas en su cumpleaños.
¿Cuántos caramelos debe poner en cada bolsita si quiere obtener el máximo número posible de bolsitas sin que le sobren caramelos?
Solución
Si el número de bolsitas es un divisor de 200 y de 175, entonces no le sobrarán caramelos: debe ser un divisor común.
Además, debe ser el máximo divisor común para obtener el mayor número posible de bolsitas.
Descomponemos los números y calculamos el mcd:
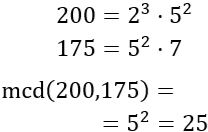
Por tanto, Carlos obtendrá 25 bolsitas.
Calculamos cuántos caramelos de cada sabor debe poner las bolsitas:
- Caramelos de fresa: 200/25 = 8
- Caramelos de limón: 175/25 = 7
Cada bolsa debe contener 8 caramelos de fresa y 7 de limón.
Problema 3
¿Cuál es el máximo común divisor de dos números primos distintos?
Solución
Si los números \(a\) y \(b\) son números primos, su descomposición como producto de potencias de primos es
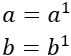
Como el mcd se calcula multiplicando las bases comunes de las descomposiciones de los números y los números son primos, no tienen bases comunes. Por tanto, su mcd es 1:
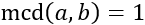
Observad que los únicos divisores de \(a\) son 1 y \(a\) (por ser primo) y los de \(b\) son 1 y \(b\) (por ser primo). El único divisor común es 1.
Problema 4
Isabel tiene un ovillo de lana de 250 metros y otro de 300 metros. Quiere cortarlos para obtener más ovillos de modo que sean lo más largos posibles y todos midan lo mismo. ¿Cuántos ovillos obtendrá Isabel y cuánto medirán?
Solución
La longitud de los nuevos ovillos debe ser divisor de 250 y de 300 para aprovechar toda la lana y que todos midan lo mismo. Además, como quiere que sean lo más largos posibles, su longitud debe ser el máximo común divisor.
Escribimos los números como productos de potencias de primos:
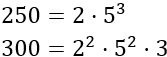
Calculamos el mcd (bases comunes al menor exponente):
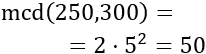
Cada ovillo debe medir 50 metros.
Isabel obtendrá 250/50 = 5 ovillos del ovillo de 250 metros y 300/50 = 6 ovillos del de 300. Un total de 11 ovillos de 50 metros.
Problema 5
- ¿El mcd de dos números puede ser mayor que alguno de estos dos números?
- ¿El mcd de dos números pares es par?
- ¿El mcd de un número par y uno impar es par?
Solución
Apartado a.
La respuesta es NO. El mcd de dos números es un divisor de dichos números, así que, como mucho, puede ser igual de grande que el menor de los números.
Apartado b.
Si un número es par, tiene una potencia de base 2 en su descomposición. Si ambos números son pares, la base 2 será una base común y, por tanto, la de menor exponente estará en el mcd. Por tanto, el mcd de dos números pares SÍ es un número par.
Apartado c.
Si un número es par, tiene una potencia de base 2 en su descomposición.
Si un número es impar, no puede tener una potencia de 2 en su descomposición ya que si la tuviera sería un número par.
Por tanto, la base 2 no es una base común y, por consiguiente, no puede estar en el mcd. El mcd no puede ser un número par.
Por ejemplo, el mcd de 20 y 25 es 5.
Problema 6
Manuel tiene dos barajas distintas: 120 cartas de Magic y 135 de Yugioh. Quiere hacer varios montones de cartas de una única baraja cada montón (sin mezclarlas). Además:
Opción 1. Si Manuel quiere que todos los montones tengan el mismo número de cartas y éste sea el mayor posible, ¿cuántos montones tendrá?
Opción 2. Si Manuel quiere tener el mismo número de montones de Magic que de Yugioh y, que éste sea máximo, sin importar que el número de cartas de los montones de Magic sea distinto al de los montones de Yugioh, ¿Cuántos montones tendrá y de cuántas cartas?
Solución
En ambas opciones Manuel tiene que calcular el máximo común divisor de 120 y 135:
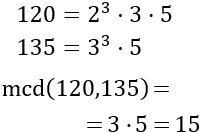
Opción 1.
El número de cartas por montón es 15. Calculamos cuántos montones tendrá:
- Cartas de Magic: 120/15 = 8 montones
- Cartas de Yugioh: 135/15 = 9 montones
En esta opción tendrá un total de 17 montones.
Opción 2.
El número de montones de cada baraja es 15. Calculamos cuántas cartas tendrán los montones:
- Cartas de Magic: 120/15 = 8 cartas por montón
- Cartas de Yugioh: 135/15 = 9 cartas por montón
En esta opción tendrá un total de 30 montones.
Problema 7
Marisa tiene un regaliz de fresa de 224 cm y uno de mora de 196. Desea cortarlos en trozos lo más grande posibles y que todos midan lo mismo. ¿Cuántos trozos de regaliz de cada sabor obtendrá Marisa?
Solución
La longitud de los trozos debe ser un divisor de 224 y 196 y tiene que ser máximo. Calculamos el mcd:
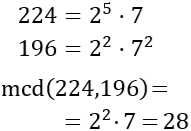
Los trozos deben medir 28 centímetros. Calculamos cuántos trozos de cada sabor obtendrá Marisa:
- Regaliz fresa: 224/28 = 8 trozos
- Regaliz de mora: 196/28 = 7 trozos
Problema 8
En el problema 3 vimos que el máximo común divisor de dos números primos es 1. Ahora supongamos que el máximo común divisor de \(a\) y \(b\) es 1, entonces ¿son primos los números \(a\) y \(b\)?
Solución
La respuesta es NO y podemos mostrarlo con un ejemplo: los números 9 y 25 no son números primos y, sin embargo, su máximo común divisor es 1.
Si el mcd de dos números es 1, se dice que los números son coprimos. Esto ocurre cuando los números no tienen bases comunes en su descomposición.
En efecto, las descomposiciones de 9 y 25 no tienen bases comunes: