Índice:
- Calculadora de mcm y mcd
- Problemas resueltos de mcm y mcd
Calculadora de mcm y mcd
Introducir 2 o 3 números para calcular su mcm y su mcd.
| Números: | |||
| mcm = | |||
| mcd = | |||
Problemas resueltos de mcm y mcd
A continuación, resolvemos 10 problemas de aplicación del mcm y mcd. Otros problemas relacionados:
- Mínimo común múltiplo
- Máximo común divisor
- Problemas teóricos de mcm y mcd
- Mínimo común múltiplo (2)
- Máximo común divisor (2)
- Problemas mixtos de mcm y mcd (2)
- Problemas mixtos de mcm y mcd (3)
Problema 1
Leo quiere comprarse unas medias de fútbol. Las de color rojo van en un paquete de 4 pares y las de color verde en uno de 6 pares. ¿Al menos cuántos paquetes debe comprar Leo para tener el mismo número de pares de cada color?
Solución
El número de pares de medias rojas que tendrá Leo es un múltiplo de 4 y el de medias verdes será múltiplo de 6. Para tener el mismo número de pares de cada color, Leo debe calcular el mcm.
Descomponemos 4 y 6:
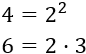
Tomamos las bases comunes y no comunes al mayor exponente para calcular el mcm:
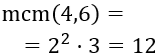
Leo tiene que comprar 12 pares de cada color. Calculamos los paquetes:
- Paquetes de medias rojas: 12/4 = 3
- Paquetes de medias verdes: 12/6 = 2
Por tanto, Leo debe comprar al menos 3 paquetes de medias rojas y 2 paquetes de medias verdes. Así, tendrá 12 pares de cada color.
Problema 2
En una competición de atrapa la bandera se van enfrentar los 48 alumnos del aula A (con peto azul) y los 36 del aula B (con peto rojo).
Se quieren hacer equipos en cada aula con las siguientes condiciones: cada equipo sólo tendrá alumnos de un aula, los alumnos solo pueden y deben estar en un único equipo, debe haber el mismo número de miembros en todos los equipos y el número de alumnos por equipo deba ser máximo.
¿Cuántos equipos habrá en total? ¿Cuántos alumnos habrá en los equipos?
Solución
Debemos calcular el mcd de 48 y 36, que será el número de alumnos por equipo.
Descomponemos los números:
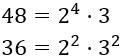
El mcd se calcula tomando bases comunes al menor exponente:
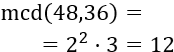
Por tanto, habrá que hacer equipos de 12 alumnos.
En el aula A, el número de equipos es 48/12 = 4, y en el aula B, 36/12 = 3 equipos.
El número total de equipos es 7 y estarán integrados por 12 alumnos cada uno.
Problema 3
Leo, Carlos y Javier están jugando a carreras de coches en un Scalextric de tres pistas. El tiempo que tarda cada uno de los amigos en dar una vuelta al circuito son dos, tres y cuatro minutos, respectivamente. Iniciada la carrera, ¿cuándo se encontrarán los tres coches al mismo tiempo en la línea de salida/meta? ¿Y la segunda vez?
Solución
Cuando se inicia la carrera comienzan a contar los tiempos.
Leo dará una vuelta cada 2 minutos; Carlos, cada 3 minutos; y Javier, cada 4 minutos. Esto significa que volverán a pasar por la línea de meta en los múltiplos de dichos tiempos.
Los coches se encuentran por primera vez en el mínimo común múltiplo de los tiempos.
Calculamos el mcm de 2, 3 y 4:
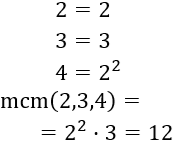
Los coches de los tres amigos se encontrarán alineados en la línea de salida a los 12 minutos.
Para hallar la segunda vez podemos buscar el menor mínimo común múltiplo que no sea el mcm:
- Los múltiplos de 2 son 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26...
- Los múltiplos de 3 son 6, 9, 12, 15, 18, 21, 24, 27...
- Los múltiplos de 4 son 8, 12, 16, 20, 24, 28, 32...
La segunda vez se produce a los 24 minutos (es decir, dos veces el mcm).
Problema 4
Paula tiene 300 abalorios de color rojo y 360 de color amarillo y quiere calcular cuántos abalorios debe poner en cada pulsera de forma que
- las pulseras deben ser idénticas, tanto en número de abalorios como de colores,
- quiere obtener el mayor número posible de pulseras,
- quiere usar todos los abalorios,
- las pulseras deben tener abalorios de ambos colores.
¿Cuántas pulseras podrá hacer Paula? ¿Cuántos abalorios tendrán las pulseras y de qué colores?
Solución
Para que no sobren abalorios, el número de pulseras debe dividir al número de abalorios de cada color. Es decir, debe ser un divisor de 300 y 360. Además, debe ser el máximo posible. Debemos calcular el mcd.
Descomponemos 300 y 360:
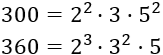
El mcd se calcula tomando los factores comunes al menor exponente:
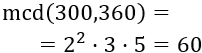
Por tanto, Paula puede hacer 60 pulseras. Calculamos el número de abalorios:
- Abalorios rojos: 300/60 = 5 abalorios por pulsera.
- Abalorios amarillos: 360/60 = 6 abalorios por pulsera.
Paula tiene que poner 5 abalorios rojos y 6 amarillos en cada una de las 60 pulseras.
Problema 5
Usar las parejas de números \(a\) y \(b\) para comprobar que se cumple la siguiente fórmula:
$$ \text{mcm}(a,b)\cdot \text{mcd}(a,b) = a\cdot b$$
Parejas de números:
- \(a = 3\) y \(b = 5\)
- \(a = 36\) y \(b = 48\)
- \(a = 90\) y \(b = 105\)
Solución
Calcularemos el mcm y el mcd de cada pareja \(a\) y \(b\) y después los multiplicaremos (el mcm por el mcd) para ver que da como resultado lo mismo que \(a\cdot b\).
Primer apartado.
Descomponemos los números:
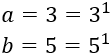
El mcm es su producto porque son números primos:
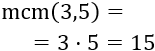
El mcd es 1 porque son números primos:
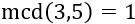
Aplicamos la fórmula:
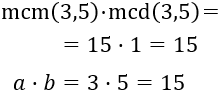
Segundo apartado.
Descomponemos los números:
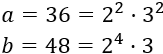
Calculamos el mcm:
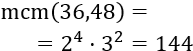
Calculamos el mcd:
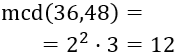
Aplicamos la fórmula:
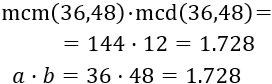
Tercer apartado.
Descomponemos los números:
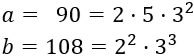
Calculamos el mcm:
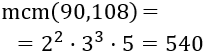
Calculamos el mcd:
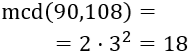
Aplicamos la fórmula:
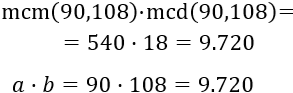
Problema 6
En una tienda deportiva hay una oferta de 2x1 en los pantalones y de 3x2 en las camisetas. Roberto quiere aprovechar la oferta para comprar el mismo número de pantalones que de camisetas, pero comprando pocas unidades para no quedarse sin ahorros. ¿Cuántas ofertas de cada tipo debe comprar Roberto?
Solución
Podemos considerar que los pantalones van en paquetes de 2 unidades y las camisetas en paquetes de 3. Roberto debe comprar un múltiplo común de 2 y 3 y, además, que sea mínimo.
El mcm de 2 y 3 es su producto, es decir, 6, porque son números primos.
Por tanto, Roberto debe comprar 6 pantalones y 6 camisetas, lo que corresponde a tres ofertas de 2x1 y dos ofertas de 3x1.
Problema 7
Ana quiere que en su fiesta de cumpleaños haya exactamente el mismo número de porciones de pizza de cuatro quesos que de pepperoni. Sin embargo, las pizzas de cuatro quesos están cortadas en 12 porciones, mientras que las de pepperoni lo están en 15 porciones. ¿Al menos cuántas pizzas tendrá que comprar Ana?
Solución
El número de porciones de cada tipo de pizza debe ser el mínimo común múltiplo de 12 y 15.
Calculamos el mcm:
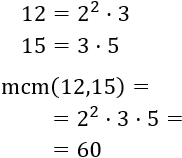
Tiene que haber 60 porciones de cada pizza. Calculamos el número de pizzas:
- Pizza de cuatro quesos: 60/12 = 5 pizzas
- Pizza de pepperoni: 60/15 = 4 pizzas
Ana tiene que comprar, al menos, 5 pizzas de cuatro quesos y 4 de pepperoni.
Problema 8
Carmen tiene un saco con 7.350 monedas de 1 céntimo y otro con 7.560 monedas de 2 céntimos y quiere dividirlos en sacos más pequeños, con idéntico número de monedas y que las monedas de cada saco sean iguales. ¿Cuántos sacos debe hacer Carmen si el número de monedas por saco debe ser máximo?
Solución
Carmen busca un divisor común de 7.350 y de 7.560. Para obtener el mayor número de monedas por saco, el divisor común debe ser el máximo posible.
Calculamos el mcd de 7.350 y 7.560:
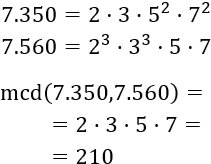
Cada saco debe tener 210 monedas.
- Sacos de 1 céntimo: 7.350/210 = 35
- Sacos de 2 céntimos: 7.560/210 = 36
El número de sacos que tendrá Carmen es 35+36 = 71.
Problema 9
María fue al parque de las fuentes y calculó que la fuente A se enciende cada 180 segundos, la B lo hace cada 150 segundos y la C, cada 108.
Si María vuelve a ir al parque a la hora del encendido de las fuentes, ¿cuántos minutos tiene que esperar para ver las tres fuentes encendidas simultáneamente?
Solución
Las fuentes se encienden en los múltiplos de los tiempos que proporciona el enunciado. La primera vez que las fuentes coinciden es en mínimo común múltiplo de los tiempos. Lo calculamos:
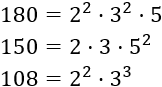
Para el mcm tomamos las bases comunes y no comunes al mayor exponente:
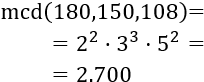
Las fuentes coinciden a los 2.700 segundos. Pasamos la cifra a minutos: 2.700/60 = 45 minutos.
María tendrá que esperar 45 minutos para ver las tres fuentes encendidas al mismo tiempo.
Problema 10
Si sabemos que el mínimo común múltiplo de dos números desconocidos \(a\) y \(b\) es 50, ¿qué números podrían ser \(a\) y \(b\)?
Solución
Hasta ahora hemos calculado el mcm a partir de \(a\) y \(b\), pero en este problema tenemos que razonar a la inversa.
Descomponemos el mcm como producto de potencias de primos:
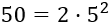
El mcm se calcula tomando las bases comunes y las no comunes al mayor exponente. Podemos hacer las siguientes observaciones:
- Las únicas bases que puede haber en las descomposiciones de \(a\) y \(b\) son 2 y 5 (además del 1, que está en todas). No puede haber otras, porque si no, lo estaría en la del mcm.
- Los números \(a\) y \(b\) pueden tener o no las bases 2 y 5 (la base 1 siempre está).
- Como el exponente de la base 2 en el mcm es 1 y en el mcm se toma la mayor base, sabemos que \(a\) y \(b\) no pueden tener una potencia de base 2 con exponente mayor que 1.
- Como el exponente de la base 5 en el mcm es 2 y en el mcm se toma la mayor base, sabemos que \(a\) y \(b\) pueden tener una potencia de base 5 con exponente 1 o 2.
Teniendo todo esto en cuenta, las diferentes posibilidades para los números \(a\) y \(b\) son las siguientes:
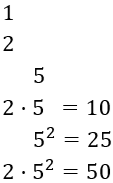
Ahora tenemos que tener en cuenta las combinaciones, dado que si, por ejemplo, \(a = 1\), entonces \(b=50\).
Escribimos un cuadro con las posibles combinaciones: