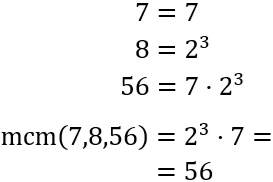Índice:
- Calculadora de mcm y mcd
- Problemas resueltos de mcm
Calculadora de mcm y mcd
Introducir 2 o 3 números para calcular su mcm y su mcd.
| Números: | |||
| mcm = | |||
| mcd = | |||
Problemas resueltos de mcm
A continuación, resolvemos 8 problemas de aplicación del mcm. Otros problemas relacionados:
- Máximo común divisor
- Problemas mixtos de mcm y mcd
- Problemas teóricos de mcm y mcd
- Mínimo común múltiplo (2)
- Máximo común divisor (2)
- Problemas mixtos de mcm y mcd (2)
- Problemas mixtos de mcm y mcd (3)
Problema 1
Calcular el mínimo común múltiplo de 6, 8, 10 y 12.
Solución
El procedimiento es el mismo tanto para 2 como para más números.
Escribimos los números como productos de potencias de primos:
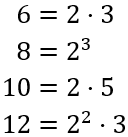
Calculamos el mcm (bases comunes y no comunes al mayor exponente):
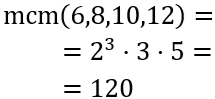
Luego el mcm de 6, 8, 10 y 12 es 120.
Problema 2
Carlos quiere comprar el mismo número de caramelos de fresa que de limón, pero los primeros vienen en bolsas de 25 unidades y los segundos en bolsas de 20. ¿Cuántas bolsas de cada debe comprar como mínimo?
Solución
El número de caramelos de fresa que tendrá Carlos será 25 multiplicado por el número de bolsas (es decir, un múltiplo de 25). El número de caramelos de limón será un múltiplo de 20.
Como Carlos quiere el mismo número de caramelos de cada sabor, éste debe ser un múltiplo común de 25 y de 20. Además, quiere que sea el mínimo posible.
Descomponemos los números para calcular el mcm de 25 y 20:
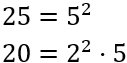
El mcm se calcula tomando bases comunes y no comunes al mayor exponente:
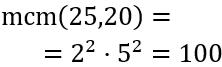
Por tanto, Carlos tendrá 100 caramelos de cada sabor.
Calculamos el número de bolsas a comprar:
- Bolsas de fresa: 100/25 = 4
- Bolsas de limón: 100/20 = 5
Problema 3
¿Cuál es el mínimo común múltiplo de dos números distintos que son primos? Pon algunos ejemplos.
Solución
Los números primos no se pueden descomponer como producto de potencias de primos. Entonces, si \(a\) y \(b\) son números primos, tenemos
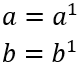
El mcm se calcula tomando factores comunes y no comunes al mayor exponente, así que
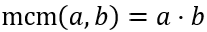
Es decir, el mcm de números primos es su producto.
Por ejemplo,
- El mcm de 2 y 3 es 6.
- El mcm de 2 y 5 es 10.
- El mcm de 3 y 5 es 15.
- El mcm de 2 y 7 es 14.
Problema 4
En una determinada parada de autobuses el autobús A pasa cada 30 minutos y el autobús B cada 45 minutos. Si el autobús A pasa a las 24:00 y es el primero del día, ¿a qué hora del día coinciden por primera vez los autobuses en la parada?
Solución
Las horas a las que pasa el autobús A son los múltiplos de 30, mientras que las del B son los múltiplos de 45.
Escribimos 30 y 45 como productos de potencias de primos para calcular su mcm:
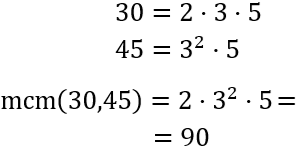
Por tanto, los autobuses coinciden por primera vez pasados 90 minutos de las 24h. Es decir, a la 1:30 am.
Problema 5
(Difícil)
- ¿Es cierto que el mcm de dos números pares es siempre par? Pon algunos ejemplos.
- ¿Y si sólo uno de ellos es par? Pon algunos ejemplos.
Solución
Apartado a.
Un número par siempre es divisible entre 2, lo que significa que en su descomposición como producto de potencias de primos tendrá una potencia cuya base sea 2.
Si tenemos dos números pares, ambos tendrán la base común 2 y, por tanto, esta también estará en su mcm (al mayor exponente). Como consecuencia, el mcm es un número par.
Ejemplos:
- 2 y 4 son pares y su mcm es 4.
- 4 y 6 son pares y su mcm 12.
Apartado b.
En este caso, el número par tendrá una potencia de base 2 en su descomposición, mientras que el impar no lo tendrá. No obstante, el mcm se calcula con bases comunes y no comunes, así que el mcm tendrá una potencia de base 2 y, por tanto, también será un número par.
Ejemplos:
- 2 y 9 son par e impar y su mcm es 18.
- 3 y 6 son impar y par y su mcm es 6.
Problema 6
María y José están entrenado el lanzamiento de dardos a diana. Como José se encuentra al triple de distancia que María de la diana, cuando da en el centro de esta se anota 30 puntos, mientas que María se anota 12.
¿Cuántos aciertos se necesitan para que la puntuación de ambos amigos sea la misma?
Solución
En primer lugar, si ninguno de los amigos acierta a la diana, entonces su puntuación será la misma: 0.
Descartando este caso, tenemos que calcular el mínimo común múltiplo de 12 y 30:
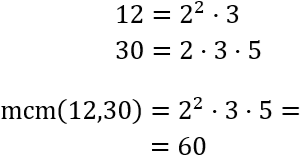
Calculamos el número de aciertos necesario para alcanzar la puntuación de 60:
- María: 60/12 = 5 aciertos.
- José: 60/30 = 2 aciertos.
Problema 7
Jaime y Teresa son artistas y están preparando una colección de cuadros. El primero de ellos completa un cuadro cada 15 días, mientras que Teresa necesita 21.
Los amigos dejarán de pintar el día en que ambos hayan terminado un cuadro (es decir, cuando hayan finalizado el cuadro en el que estaban trabajando). ¿Qué día será? ¿Cuántos cuadros habrán pintado?
Solución
Tenemos que calcular el mínimo común múltiplo de 15 y 21:
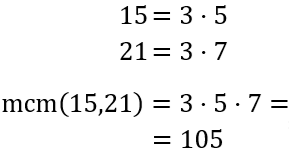
Deben pasar 105 días. Calculamos cuántos cuadros han pintado:
- Jaime: 105/15 = 7 cuadros.
- Teresa: 105/21 = 5 cuadros.
Problema 8
Si \(m\) es el mínimo común múltiplo de \(a\) y \(b\), ¿cuál es el mínimo común múltiplo de \(a\), \(b\) y \(m\)? Pon un ejemplo.
Solución
Sabemos que \(m\) es el menor de los múltiplos comunes de \(a\) y \(b\). Además, \(m\) es múltiplo de \(m\) porque
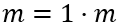
Y es el menor de los múltiplos de \(m\).
Por tanto, \(m\) es el menor de los múltiplos de \(a\), \(b\) y \(m\). Es decir, es el mínimo común múltiplo de \(a\), \(b\) y \(m\).
Por ejemplo, consideremos los números 7 y 8. Su mcm es 56.
El máximo común divisor de 7, 8 y 56 es 56: