Índice:
- Calculadora de mcm y mcd
- Problemas teóricos resueltos
Calculadora de mcm y mcd
Introducir 2 o 3 números para calcular su mcm y su mcd.
| Números: | |||
| mcm = | |||
| mcd = | |||
Problemas teóricos de mcm y mcd
Problemas teóricos resueltos (demostraciones) sobre mínimo común múltiplo y máximo común divisor: 10 propiedades y fórmulas.
- Mínimo común múltiplo
- Máximo común divisor
- Problemas mixtos de mcm y mcd
- Mínimo común múltiplo (2)
- Máximo común divisor (2)
- Problemas mixtos de mcm y mcd (2)
- Problemas mixtos de mcm y mcd (3)
Problema 1
El mínimo común múltiplo de dos números primos distintos es igual a su producto.
Demostración
Los números primos no pueden descomponerse como producto de varias potencias de números primos. La única posibilidad para descomponer dos números primos \(a\) y \(b\) es
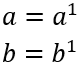
Nota: técnicamente, también podemos escribir el 1 en la descomposición:
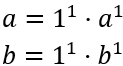
El mínimo común múltiplo (mcm) se calcula multiplicando las bases comunes y no comunes al mayor exponente. Si dos números son primos distintos, no tienen bases comunes, por tanto, su mcm será su producto:
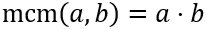
Por ejemplo, el mcm de los números primos 7 y 23 es 161.
Problema 2
El máximo común divisor de dos números primos distintos es 1.
Demostración
Razonando como en el problema anterior, la descomposición de los primos \(a\) y \(b\) es
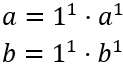
El máximo común divisor (mcd) se calcula tomando las bases comunes al menor exponente. En este caso, la única base común es 1, así que su mcd es 1:
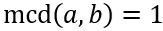
Problema 3
El mínimo común múltiplo y el máximo común divisor de dos números pares son números pares.
Demostración
Supongamos que \(a\) y \(b\) son número pares. En este caso, necesariamente 2 es un divisor suyo y, por tanto, ambos números tienen una base de 2 en su descomposición.
Independientemente de su exponente, 2 es una base común, por lo que estará tanto en el cálculo de su mcm como de su mcd. Como consecuencia, el mcm y el mcd serán pares.
Por ejemplo, consideremos los números
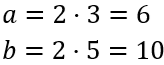
Su mcm y su mcd son números pares:
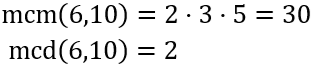
Problema 4
El mínimo común múltiplo de un número par y de uno impar es un número par. Sin embargo, su mcd es impar.
Demostración
Razonando como en el problema anterior, el número par tiene una potencia de base 2 en su descomposición.
El número impar no puede tener una potencia de base 2 en su descomposición porque, en caso de tenerla, sería un número par (y no impar).
En el cálculo del mcm tomamos las bases comunes y las no comunes, lo que incluye la base 2. Como consecuencia, el mcm es un número par.
Sin embargo, el mcd se calcula tomando únicamente las bases comunes. El 2 no es una base común porque sólo aparece en la descomposición del número par. Por tanto, no hay una potencia de base 2 en la descomposición del mcd y, como consecuencia, el mcd no es par. Si el mcd no es par, es impar.
Problema 5
El mínimo común múltiplo y el máximo común divisor de dos números impares son impares.
Demostración
Razonando como en los problemas anteriores, no hay ninguna potencia de base 2 en las descomposiciones de los números impares. Luego no es una base común ni no común, así que no estará ni en el mcm ni en el mcd. Como consecuencia, el mcm y el mcd son impares.
Problema 6
Si \(a \geq b\), entonces
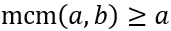
Y, también,
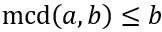
Dicho en palabras: el mcm de dos números es igual o mayor que el mayor de dichos números y el mcd es menor o igual que el menor de dichos números.
Demostración
El mínimo común múltiplo es un múltiplo de \(a\) y de \(b\) y, por tanto, necesariamente es mayor o igual que ambos:
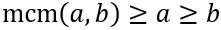
El máximo común divisor es el mayor de los divisores de \(a\) y de \(b\), así que no puede ser mayor que dichos números:
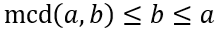
Por ejemplo, el mcm de 4 y 6 es 12, mayor que ambos números. Y su mcd es 2, menor que ambos números.
Problema 7
Si \(b\) es un múltiplo de \(a\), entonces el mínimo común múltiplo de \(a\) y \(b\) es \(b\) y el máximo común divisor es \(a\).
Demostración
Si \(b\) es múltiplo de \(a\), existe un número natural \(n\) de modo que
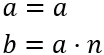
Es fácil ver que el mínimo común múltiplo de los números es \(b\) (es el primer múltiplo común) y que el mayor de los divisores de ambos es \(a\).
Por ejemplo, consideremos los números 8 y 40:
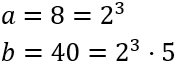
Calculamos su mcm y su mcd:
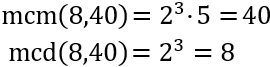
Problema 8
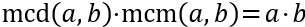
Demostración
Consideremos el conjunto de todos los números primos, ordenados de menor a mayor:
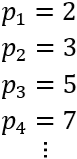
Dados dos números \(a\) y \(b\), podemos escribir sus descomposiciones como producto de potencias de todos los números primos:
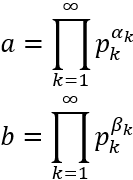
Por ejemplo, si
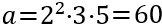
Entonces, \(\alpha _1 =2\), \(\alpha _2 =1\), \(\alpha _3 =1\) y \(\alpha _n =0\) para todo \(n \geq 4\).
El producto de \(a\) y \(b\) es
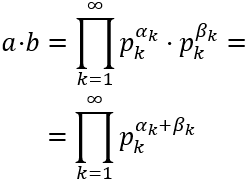
Como el mínimo común múltiplo se calcula tomando las bases comunes y no comunes al mayor exponente,
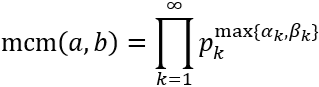
Como el máximo común divisor se calcula tomando las bases comunes al menor exponente,
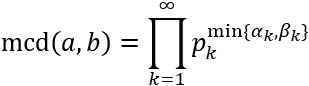
El producto del mcm y del mcd es
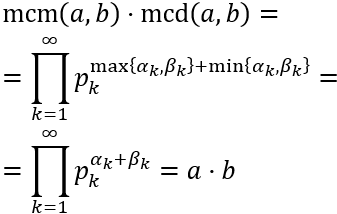
Nota: obsérvese que la suma del máximo y el mínimo de dos números es la suma de ambos números.
Problema 9
Sea \(n\) un número natural. Entonces,
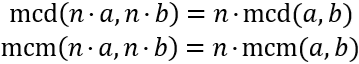
Demostración
Usando la notación vista en el problema anterior, consideremos las descomposiciones de \(a\) y \(b\):
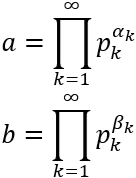
El número natural \(n\) también podemos escribirlo de este modo:
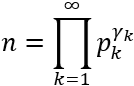
En el problema anterior ya vimos que el mcd de \(a\) y \(b\) es
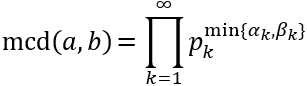
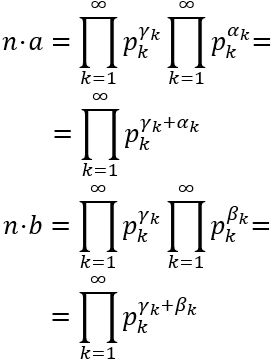
Las descomposiciones de los números \(n\cdot a\) y \(n\cdot b\) son
Calculamos el mcd de estos dos números:
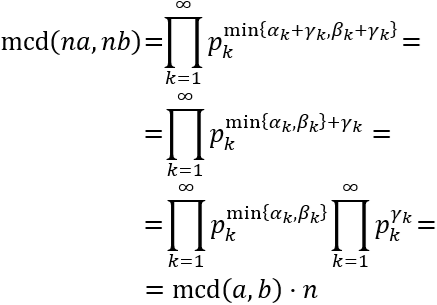
La demostración para el mcm es análoga.
Problema 10
Sea \(d\) un natural divisor de \(a\) y \(b\). Entonces,
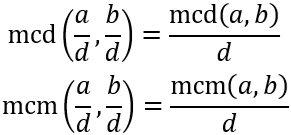
Demostración
Utilizamos las mismas descomposiciones y notación que en los problemas anteriores. Consideremos también la descomposición del divisor \(d\):
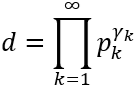
Como \(d\) es divisor de \(a\) y \(b\), los exponentes \(\alpha _k\) y \(\beta _k\) son mayores o iguales que \(\gamma _k\).
Por tanto, podemos escribir
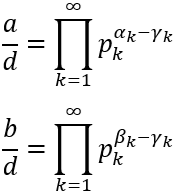
Ya vimos que el mcd de \(a\) y \(b\) es
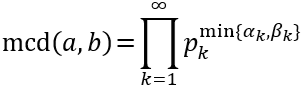
Calculamos el de \(a/d\) y \(b/d\):
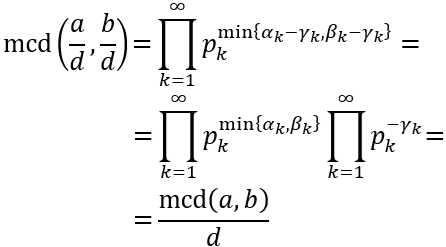
La demostración para el mcm es análoga.